Notions fondamentales et classiques en probabilité

Les probabilités et particulièrement les probabilités discrètes ont tendance à faire peur aux étudiants. Pourtant, avec un travail méthodique et de la régularité vous verrez que c’est un tiers du programme qui n’est pas si compliqué et que pas mal de points sont à gagner. L’objectif de cet article est de mettre en avant les points de cours mais également certains raisonnements classiques à maîtriser car ils font partie des classiques au concours. Les probabilités discrètes et les densités seront traitées séparément à part pour la première partie.

Généralités sur la probabilité

• La première chose à savoir et à ne pas oublier en probabilité c’est qu’une probabilité se situe sur un intervalle entre 0 et 1. Une probabilité proche de 1 permet de conclure que l’événement calculé par la probabilité est sûr, et donc qu’il a de fortes chances de se produire alors que plus la probabilité se rapproche de 0 plus l’événement est moins sûr. Cela peut être utilisé notamment lorsqu’une question au concours propose d’analyser un résultat du type « que pouvez-vous en conclure ? » après avoir calculé la probabilité d’un événement. De plus, cela peut être utile pour étudier des limites ou des fonctions.
• Pour réussir en probabilité, il faut maîtriser les différentes méthodes calculatoires notamment à base de séries et d’intégrales. Lire plus : Astuces quand on a du mal à décoller en mathématiques/
• Une loi de probabilité vaut 1.

Les probabilités discrètes

D’abord jetons un œil aux applications direct du cours :

• Trouver l’espérance et la variance: il y a 2 méthodes soit c’est une formule classique du cours soit vous devez calculer « E(X) = k.P[X=k]) » pour l’espérance et montrer la convergence. Pour avoir la variance la méthode est un peu plus longue mais pas plus dure il suffit de faire « E(X^2) = k^2P([X=k]) » puis il faudra utiliser la formule de Koenig-Huygens et citez sur votre copie son nom car une partie des points est sur la capacité à citer le théorème utilisé. Pour rappel Koenigs-Huygens : V(X) = [(E(X^2)-E(X)^2]
• Répondre à la question « montrer que P([X=k]) est une loi de probabilité » : une loi de probabilité par définition est égale à 1, il faut donc faire la somme de tous les événements qui sont pris par la loi de probabilité soit si vous concluez ainsi, vous avez bien montré que P([X=k]) est une loi de probabilité. Important à savoir, ce résultat peut être réutilisé dans des questions qui vont suivre
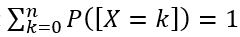
• Que faire quand on a une suite de probabilité ?: Une suite de probabilité est souvent donnée telle que Un = P([X_n=k]). On va essayer de comprendre grâce à un exemple, par exemple Un = P([X_n=0])
• Le calcul des premiers termes de la suite : il suffit de remplacer l’indice « n » en fonction du Un, ainsi U₀ = P([X₀=0]). Là il suffit d’analyser est-ce que cet événement est possible ? Si oui, il faut le calculer, l’idée c’est de savoir le modéliser donc aidez-vous d’un dessin ou autre.
• Montrer qu’elle converge : pour cela une méthode possible est d’utiliser un autre événement, par exemple U_n et U_n+1 ensuite, il suffit de raisonner par inclusion. C’est-à-dire regarder si la réalisation de l’événement [X₀=0] implique celle de [X₁=0]. Pour cela pas de panique, pour comprendre, expliquez en quelques ligne ce qui signifie chacun des événements et vous trouverez la réponse. Si on a bien [X₀=0] ⊂ [X₁=0] on obtient par croissance de la probabilité P([X₀=0]) ≤ P([X₁=0]) soit U₀ ≤ U₁ donc plus généralement on a U_n ≤ U_n+1 par conséquent, la suite est croissante. A présent comment montrer la convergence de la suite ? rappelons-nous que nous sommes dans le domaine des probabilités ce qui signifie que la limite « L » est comprise dans l’intervalle [0 ;1] le théorème de la limite monotone nous assure grâce à la croissance et à la majoration 1 que la suite U_n est convergente.

Les densités de probabilité

Concernant les points de cours fondamentaux à connaître et plus particulièrement les écritures (qui ont un rôle important) vous pouvez vous entraîner sur le sujet EML 2022 ECE. Cet exercice retrace les fondamentaux des densités et montre comment certains résultats du cours peuvent être appliqués. Par exemple, le fait qu’une densité soit égale à 1 permet de réaliser des encadrements, cela peut être très utile notamment pour calculer des limites. Il est aussi important de voir la tram qui se dessine. En règle générale, vous commencez souvent par calculer une intégrale et vous devez vérifier si elle est bien une densité, puis on vous demandera de calculer la fonction de répartition et souvent, l’exercice se finit par un transfert de loi à calculer en fixant le x et en faisant tendre n vers les bornes de votre fonction de votre fonction de répartition. Voilà 3 points fondamentaux à savoir faire en densité car les méthodes sont récurrentes, c’est donc des points abordables.