Le dilemme du prisonnier dépeint une situation où deux joueurs auraient collectivement intérêt à coopérer mais finissent par se trahir en raison de leur intérêt propre. Célèbre en économie car traitant des ententes illégales, ledit dilemme s’étend à divers autres domaines tels que les sciences politiques et la psychologie.
Optimum de Pareto, équilibre de Nash, matrice des paiements… cet article illustre les notions clés de la théorie des jeux pour que le dilemme du prisonnier n’ait plus de secrets pour toi !
A l’origine du dilemme du prisonnier
Alors qu’ils travaillaient pour la RAND Corporation, une société de conseil et de recherche américaine, les deux mathématiciens Melvin Dresher et Merrill Flood sont les premiers à avoir expérimenté le dilemme du prisonnier. Peu de temps après, en 1950, Albert W. Tucker l’interprètera et formulera alors le problème comme suit :
« Deux complices d’un crime sont interrogés séparément par la police qui leur fait la même offre : si les deux coupables se dénoncent, ils écoperont de 5 ans de prison. Si l’un dénonce son complice sans qu’il ne le dénonce, le premier sera libre et le second aura 10 ans de prison. Si personne ne se dénonce, les deux auront 6 mois de prison. »
Afin de modéliser le dilemme, on utilise souvent une matrice des paiements, un tableau résumant les gains et les pertes de chaque joueur en fonction des actions réalisées.
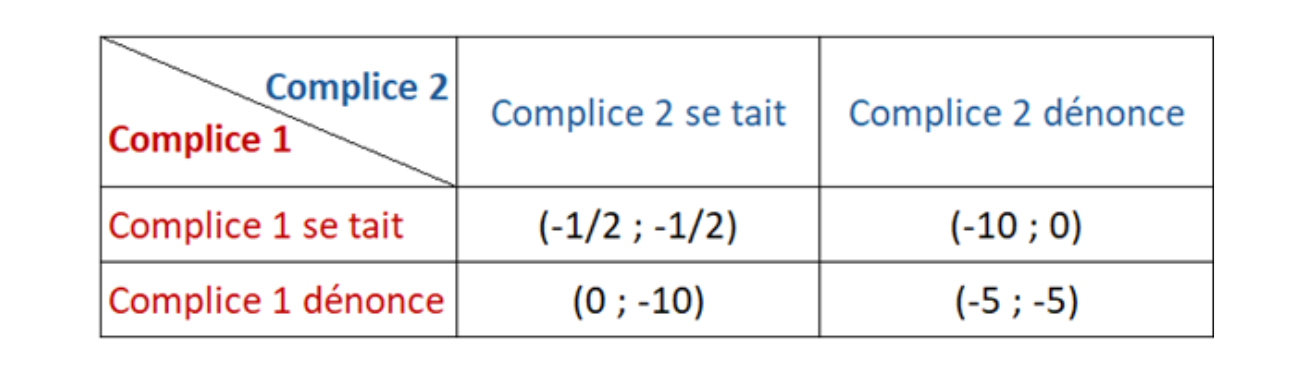
Naturellement et compte tenu des sanctions, l’entraide (ne pas se dénoncer) semble être le meilleur choix. Pourtant, ce n’est jamais la stratégie adoptée par les joueurs.
Comprendre les choix et motivations des joueurs
La principale caractéristique du dilemme du prisonnier est qu’il s’agit d’un jeu simultané (chaque joueur joue en même temps et selon les choix adverses) et à somme non nulle (la somme des gains varie)… ce qui implique a fortiori la rationalité des joueurs !
Pour bien comprendre comment se manifeste cette rationalité, incarnons un instant le Complice 1 et estimons les choix qui s’offrent à lui grâce à un arbre pondéré.
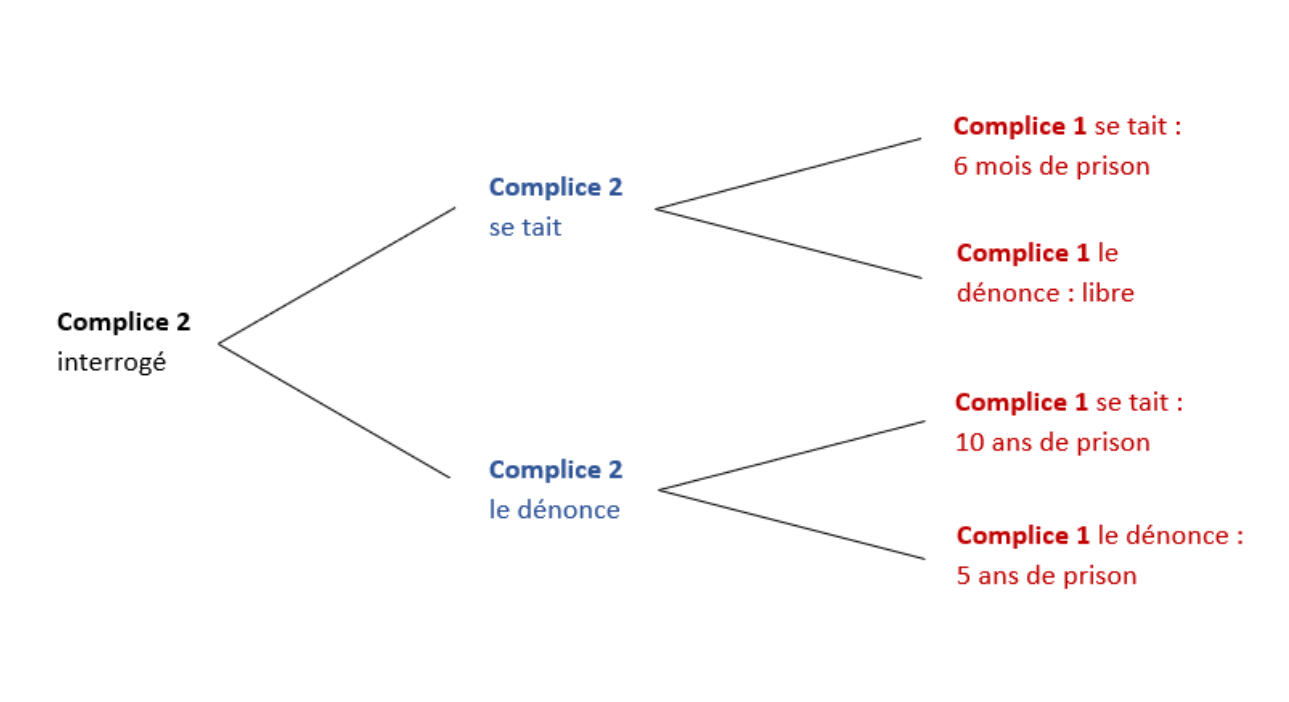
Peu importe le choix du Complice 2, le Complice 1 sera toujours sanctionné par une peine moins lourde en dénonçant son allié. L’intérêt d’une telle préférence se justifie donc par un certain égoïsme des joueurs lié à un manque de coopération d’une part et par une vraie rationalité d’autre part, le coopératif étant toujours plus sanctionné que le traître.
Lire plus : Théorie des jeux : applications pratiques d’une théorie économique – MP
Des équilibres… déséquilibrés ?
Après avoir analysé les comportements des joueurs, révéler son acolyte s’avère sensé. Toutefois, un point reste latent : si la rationalité est invoquée, n’est-il pas précisément plus judicieux de coopérer ? Rappelons que si les deux criminels se taisent, ils ne seront condamnés qu’à 6 mois de prison. Ce dernier choix est ce que l’on appelle un optimum de Pareto : il devient impossible d’augmenter la satisfaction d’un agent sans diminuer celle d’au moins un autre.
Cependant, comme démontré précédemment, la rationalité des joueurs prend le dessus et tend à obscurcir ledit équilibre qui devient inatteignable. En l’absence de coopération et de communication, et malgré un résultat global moins favorable, la trahison devient inévitablement la stratégie dominante. C’est un équilibre de Nash, une situation dans laquelle chaque joueur maximise son gain compte tenu de la bonne prévision des actions de l’autre joueur. Certes, cet équilibre est sous-optimal selon Pareto car il y a un intérêt collectif à respecter l’accord de se taire. Or, chaque coupable a individuellement intérêt à dénoncer l’autre et puisqu’in fine, le jeu devient non coopératif, les joueurs ne regrettent jamais leurs choix, bien que le résultat soit perdant-perdant.
Un dilemme chimérique ?
Notons que le dilemme du prisonnier a souvent été critiqué par son aspect trop théorique, ignorant nombre d’hypothèses menant à sa remise en cause.
D’une part, si le dilemme s’applique effectivement à des cas concrets, celui-ci peut être aisément écarté. Le cas des politiques environnementales est à cet égard patent. Si les gouvernements n’ont initialement aucun intérêt à les mener, cette logique probabiliste est perturbée par des mouvements citoyens qui mobilisent ainsi l’opinion publique.
D’autre part, pour mieux traduire la réalité, des conditions ambigües du modèle sont altérées. Jeu fini, gains non incitatifs, duel… D’autres modèles ont ainsi été développés en considérant une série de répétition de choix (dilemme itératif du prisonnier), en modifiant les gains (jeu de la poule-mouillée) ou le nombre de joueurs (dilemme à plusieurs joueurs).
Le dilemme du prisonnier ne doit toutefois pas s’interpréter comme un outil limitant immanquablement la coopération. Au contraire, il s’inscrit comme une conjecture dépendant de schémas et d’hypothèses mathématiques décrivant une inaction potentielle. Il est donc un puissant outil pour anticiper les paralysies de choix et prendre les meilleures décisions possibles.






















Vous devez être connecté pour poster un commentaire.