Mathématiques

5 astuces sur les séries en mathématiques

En analyse, il est très fréquent que vous vous retrouviez devant une question du type “Déterminer la nature de cette série”, ou “Cette série est-elle convergente ?”. Mister Prépa vous propose une liste de 5 astuces sur les séries en mathématiques qui vous rendront capable de traiter ce type de question le jour des concours !

Lire plus : Avoir 20/20 à chaque épreuve de maths (copies à l’appui)

Mais avant d’utiliser ces astuces pour déterminer la nature d’une série, je vous conseille d’abord de vérifier ces 3 étapes :

Vérifier si la limite du terme général de la série tend vers 0. En effet : si la série ∑u_n converge, alors la limite de u_nest égale à 0. Ainsi, par contraposée, si la limite de u_n est différente de 0, alors la série de terme général u_ndiverge.
Vérifier que la série que vous étudiez n’est pas une série de référence. Dans votre cours sur les séries, il existe 3 types de séries de référence : les séries géométriques, les séries exponentielles et les séries de Riemann.
Vérifier que vous ne pouvez pas majorer ou minorer la série que vous étudiez. En effet :
- Si c’est une série à termes positifs, vous pouvez facilement montrer que la somme partielle est croissante. Or si vous arrivez à majorer la somme partielle (pour tout n), alors d’après le théorème de convergence monotone, votre série converge.
- Si c’est une série à termes négatifs, vous pouvez facilement montrer que la somme partielle est décroissante. Or si vous arrivez à minorer la somme partielle (pour tout n), alors d’après le théorème de convergence monotone, votre série converge.

Astuce n°1 : Penser à utiliser les théorèmes de comparaison de séries

Dans votre cours sur les séries, il existe 3 théorèmes de comparaison :

Le théorème de comparaison par inégalité
Le théorème de comparaison par équivalence
Le théorème de comparaison par négligeabilité

Ces théorèmes sont très utiles pour déterminer la nature d’une série ! Même s’il est parfois difficile de repérer quel théorème utiliser, vous aurez plus de facilité avec un peu d’entraînement !

Je vous propose 2 exemples :

Dans ce premier exemple, il semble difficile d’utiliser le théorème de comparaison par inégalité ou par négligeabilité. On opte donc pour le théorème de comparaison par équivalence, qui est ici adapté !

Ce deuxième exemple est une question très classique sur les séries, notamment dans les sujets EDHEC et emlyon. A chaque fois que vous devez faire face à une série avec un « exponentielle puissance moins quelque chose » en terme général, pensez à cette astuce ! Il faut utiliser le théorème des croissances comparées avec n² (ou n^y avec y >1), puis utiliser le théorème de comparaison par négligeabilité avec une série de Riemann convergente !

Astuce n°2 : Penser à utiliser les sommes télescopiques

Une « somme télescopique » est une somme dont les termes s’annulent de proche en proche. Par exemple, (a₁-a₀) + (a₂-a₁) = a₂-a₀

Si (a_n) est une suite numérique, la série télescopique correspondante est la série de terme général a_n+1 – a_n. On a alors :

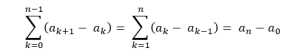
Ainsi, la convergence de la série télescopique ∑(a_n+1– a_n) équivaut à la convergence de la suite (a_n) :

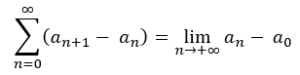
Par exemple :

Astuce n°3 : Vérifier si la série est une série alternée

Cette astuce est très spécifique à des séries alternées, c’est-à-dire des séries de la forme :

Dans ce cas, la série converge tout le temps ! Cependant, puisque ce n’est pas un théorème au programme, il faudra toujours le démontrer.

La démonstration est assez rapide :

Comme vous le voyez ici, la démonstration demande de connaître la définition de 2 suites adjacentes. Pour rappel, 2 suites sont dites adjacentes lorsque :

Une des deux suites est croissante
L’autre est décroissante
La limite de la différence des 2 suites en +∞ est nulle.

Astuce n°4 : Penser à la comparaison série-intégrale

Principe de la comparaison série-intégrale :

Ainsi ici, si on connait la primitive de f, on peut comparer les sommes partielles avec la primitive. En faisant tendre n vers +∞, on pourra alors comparer la série avec la limite en +∞ de cette primitive. Autrement dit, on pourra déterminer la nature de la série étudiée par comparaison avec la limite de la primitive de f en +∞.

Pour que ce soit plus clair, voici un exemple classique :

Cette méthode est très classique. Pour preuve, il a fallu l’utiliser cette année pour l’épreuve ECRICOME et pour la Maths II HEC/ESCP en maths approfondies !

Lire plus : Maths 2 Approfondies ESCP/HEC 2024 – Analyse du sujet